We’ll show you around some of the tools you need for rolling out your own high-performance cluster.
HPC Toolbox
Early parallel computers were typically designed as Symmetric Multiprocessor (SMP) systems with shared memory. With a large number of processors, the SMP layout quickly led to technical difficulties, which in turn necessitated a distributed hardware layout. It is difficult to implement (at least virtual) centralized memory for the large numbers of processors in a distributed system, so SMP increases the complexity of the hardware. At the same time, the design is extremely prone to error, which restricts the maximum size of a system. In contrast, a cluster doesn’t have centralized memory; instead, it relies entirely on message-based communications between its individual computers, or nodes. A group of computers becomes a cluster thanks to special tools, most of which are free on Linux.
Nearly all the supercomputers built and operated today are clusters. If they comprise standard components, they are referred to as commodity clusters – the other supercomputers are based on specially developed components. For example, the widespread Blue Gene supercomputers use a connecting network that was specially developed for use with Blue Gene systems.
Cluster Setup
The clustering model was originally introduced by Datapoint, but it wasn’t until the early 1980s that DEC had some initial commercial success with its VAX cluster. The Linux operating system made a decisive contribution to reducing the costs of supercomputers with the invention of the Beowulf cluster (Figure 1). Today, every university can afford a cluster.
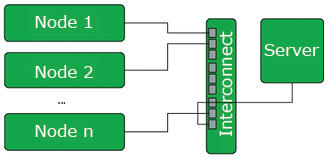 Figure 1: The Beowulf cluster model is simple: one server and multiple nodes, all of which are connected by a network.
Figure 1: The Beowulf cluster model is simple: one server and multiple nodes, all of which are connected by a network.
The basic idea behind Beowulf is to let the user build a high-performance cluster from ordinary hardware and mostly free, open source software. The basis of a cluster of this kind is a central server that provides services, such as DHCP and the network filesystem, while at the same time serving as a login front end. Interactive users will log in to this system to access other nodes in the cluster.
The most important components in a cluster are the nodes – this is where the actual workload is handled. It is a good idea to have a large number of nodes, but they only need a minimal hardware configuration. Nodes don’t actually need identical hardware, but the software installed on them has to be identical throughout the cluster. And, if you have a large cluster, it is definitely useful to have identical hardware for all your nodes.
Interconnecting
The cluster operator needs to connect all of the distributed components. In the simplest case, you can just use legacy Ethernet – and this is the approach used with the early Beowulf clusters. Although Ethernet can achieve data rates of up to 10GB per second, the latency values (i.e., the time a data packet needs to be transmitted) are a lot worse.
The main reason is that the data packet first has to navigate the many layers of the TCP/IP stack before communication can take place. This limitation explains why today’s cluster providers have special interconnects, such as Infiniband or Myrinet, which were designed for latency-critical applications, and which are also on sale as standard components.
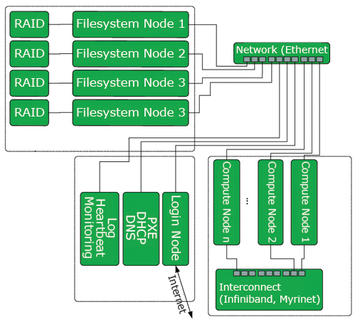 Figure 2: Today’s clusters use a more complex model. Computational nodes are connected with a fast interconnect; special filesystem nodes provide the distributed filesystem. Services are offered by multiple machines.
Figure 2: Today’s clusters use a more complex model. Computational nodes are connected with a fast interconnect; special filesystem nodes provide the distributed filesystem. Services are offered by multiple machines.
Modern cluster systems often extend the original Beowulf model (Figure 2). In addition to the computational nodes, these systems also have login nodes that the operator can use to compile the programs the cluster executes. For this reason, larger systems with many users also have multiple login nodes. As the number of nodes increases, the services are distributed over multiple physical machines. When this happens, a separate server is required to monitor the cluster. This server centrally stores all the log data, uses a heartbeat service to regularly check if all of the nodes are responding to requests from the network, and provides special monitoring software that gives the administrator the details of the current system load. It is important to monitor the nodes, because a single failed node can take down a program running in the cluster.
Booting Off the Network
A PXE network boot server that provides DHCP and DNS at the same time removes the need for hard disks on the nodes, thus improving availability. This configuration eliminates the need for a hard disk in each node because the payload data is typically stored on a parallel filesystem. Another group of servers provides the filesystem nodes. The filesystem nodes make up what is essentially a cluster within a cluster to handle the exacting requirements that occur due to parallel file access. At the same time, this means the system software for the clustering filesystem itself comprises parallel programs. To achieve a high data rate and a certain degree of availability, the data should be stored on RAID systems in the background.
Linux as a High-Performance Operating System
Computer experts, or in fact anybody who is interested in doing so, can check out the biannual top 500 list to discover which are the fastest computers in the world. One thing you might notice about the list is the fact that most of these systems run on Linux. SUSE Linux Enterprise (SLES) and Red Hat Enterprise Linux (RHEL) are popular options – SLES because of its ties with the IBM Blue Gene series, and RHEL because it is very popular with North American customers.
At first glance, it may seem a little conservative to opt for a commercial enterprise Linux variant, but buying a large cluster typically involves investing millions, and any failure will cost a lot of money. Vendors assume that the enterprise Linux versions have been thoroughly tested and are thus a safer option. Other distributions exist for small to medium-sized cluster projects.
If you are interested in exploring the world of high-performance competing without breaking the bank, you can use special live distributions that combine general-purpose computers to create a cluster. The pioneers in this field were distributions such as Cluster and Parallel Knoppix. Neither of these projects is currently under active development, although PelicanHPC is an actively maintained successor to Parallel Knoppix.
Besides the enterprise Linux options, some special cluster distributions exist that traditionally run on the hard disks in the nodes. Rocks, which is based on CentOS (itself an RHEL clone), is a free variant that comes with the software required for parallel computing. Additionally, you can install Rocks on multiple nodes at the same time thanks to a special installer (see Table 1).
| Name | Type | URL |
| SLES | Installed | http://www.suse.com/products/highavailability/ |
| RHEL | Installed | http://www.redhat.com/rhel/ |
| Rocks | Installed | http://www.rocksclusters.org |
| PelicanHPC | Live | http://idea.uab.es/mcreel/ParallelKnoppix |
| BCCD | Live | http://bccd.net |
| ABC Linux | Live/Netboot | http://www.ehu.es/AC/ABC.htm |
Besides the commercial and specialist distributions, almost any standard Linux distribution is suitable for running a cluster. In most cases, all you need to do on a popular distribution such as openSUSE, Debian, or Gentoo is add some repositories containing the special-purpose software.
Installation
Installation is a task that you should never underestimate whatever cluster you manage. Although installing the system software manually on a single machine is quite easy, going through these steps on several hundred nodes could take months.
A really simple approach is to use netboot servers, where the whole system software boots directly off the network. A PXE server can manage the netboot process. PXE alternatives include Open Bootrom or EFI. Netboot is particularly advantageous in very large installations because the nodes can do without hard disks. This approach saves power and removes a potential source of error. But, even if you have a smaller installation, this kind of setup will help you minimize maintenance costs and let you turn computers that act as desktops during the daytime into cluster nodes at night.
If the system software for the nodes doesn’t fit in a RAM disk, or if other technical reasons prevent the setup without hard disks, you will need to find an approach to distributing the Linux installation. One technical reason could be that an application you want to run on the cluster needs a large local disk. Local installations of this kind are handled by network-capable installers such as Fully Automatic Installation (FAI [1]). FAI was developed to automate the process of installing Debian, but it is also capable of installing other Debian-based distributions in a distributed way.
RPM-based distributions typically have their own network-capable installers. For example, you can install Red Hat-based distributions with Kickstart and SUSE-based distributions with Yast. With a network-based installation, the installation server can quickly become a bottleneck if the number of nodes is extremely large.
Another elegant variant on the local installation of the cluster is to use imaging software. You don’t need to run an installer to install the distribution on every single node; instead, you replicate an existing installation on one node to all your other nodes. This method eliminates the need for a package management system provided by the distribution. Installing an image also increases the accuracy of preliminary testing on a test cluster, because the production systems are 100% identical.
Partimage [2] is an easy-to-use imaging tool that backs up and restores different types of partitions. SystemImager [3] is far more mature and capable; besides the installation process, it also lets you configure the installation you create. Additionally, SystemImager can retrieve its data from a local BitTorrent network, thus removing the bottleneck of the server-based installation.
Administration
After installing the cluster, you’ll need a way to manage it. SSH is the tool that is mostly used for remote cluster management. Of course, you could manage a single server easily and conveniently with VNC, but to roll out the same change simultaneously on 100 nodes, you need some kind automation, and VNC is not easy to script. In many cases, administrators turn to projects such as Parallel SSH [4] to handle SSH automation for cluster administration.
Another important part of administration is hardware monitoring to identify an imminent failure. The lm_sensors tool [5] lets you monitor the fan and temperature. With just a little scripting, you can even create a heat map of the cluster to identify hotspots.
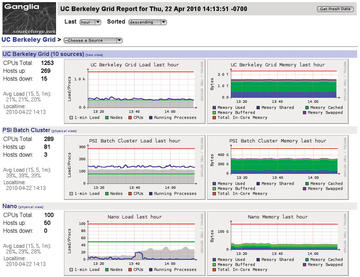
The smartmontools [6] set does similar things for hard disks, if you need to make sure your disks are running within a specified temperature range. Too low a temperature can also accelerate the demise of a hard disk. The legacy top tool is not capable of giving you an overview of the programs running on a cluster. In this case, you need some kind of distributed monitoring software. Ganglia [7] is a distributed monitoring tool for high-performance computers ( Figure 3).
Parallel Filesystems
A network filesystem is necessary for distributed, high-availability storage of your data. Network filesystems are easily installed on a RAID system, which gives you additional protection against hard disk failure. A parallel filesystem must fulfill special requirements; after all, in a cluster every single node could and possibly will access the filesystem at the same time. Fortunately, Linux is well-equipped with on-board tools to help you handle application scenarios like this. The software RAID subsystem integrated into the kernel [8] can handle most RAID modes and can almost keep pace with most hardware-based solutions. At the same time, the pool of available storage can be managed dynamically using LVM2 [9]. With these two tools, you have a very inexpensive approach to implementing the filesystem nodes that form the basis of your storage cluster.
Linux users can choose among numerous parallel filesystems, many of them built into the kernel. Probably the best known is CIFS, which recently learned to support clusters. The Red Hat-approved Global File System 2 (GFS2) is also built directly into the kernel and was designed for use in clusters from the outset.
Another option is Oracle File System 2 (OCFS2), which is also built into recent Linux kernels. A really hot candidate for a high-performance and free cluster file system is CEPH [10] which was introduced in kernel 2.6.34.
Job Control
Once you have a plan for installing, booting, and monitoring your HPC cluster, you need to ask who will be running which programs on the cluster, and how you will coordinate requests from users. The software that launches a parallel program on the cluster is known as a batch system or job control. Such systems [1] are classified into two categories: queue-based and plan-based systems.
A program executing on a cluster is referred to as a job. Users need to tell the batch system how many nodes they need and whether to run the job as a batch job or in interactive mode. If the program is a batch job, the system normally needs a script to launch the program.
Queue-based systems are the most popular type of job control in clusters. Requests for the required resources are assigned slots in the queue. Queue systems then process the jobs based on criteria such as size, priority, and order of submission. One of the older systems is the Portable Batch System, which was developed by NASA in the 1990s. An open source version is available as OpenPBS [11]. That said, however, the Torque [12] variant, which is also free, is far more popular today.
Plan-based systems give the user the ability to reserve parts of the cluster in advance. When users submit a job to a system of this kind, they also have to define when to run the job. This feature is best suited to interactive jobs for which a user wants to reserve sufficient nodes. OpenCCS [13] is an example of this kind of system.
Standard Software
I can imagine that many people who need to handle a task that requires an HPC system will not relish the idea of parallel programming. It is always worthwhile to check whether a useful piece of software already exists for the problem. If a program needs the Message Passing Interface (MPI), or is at least capable of using MPI, this is a good indication that the software is capable of running on the cluster.
DistCC [14] is an example of a project that provides a distributed compiler. This kind of compiler saves money because developers don’t need to wait while the program builds. If you need to compute number-crunching-style statistics on a cluster, the free S-Plus clone, R [15], is a useful choice.
Finite Element Method (FEM) programs are used throughout the field of physical and mechanical simulation. Elmer [16] is a free program that can use FE methods to simulate global and structure mechanics, and it is cluster capable.
Another field in which simulation is used heavily benefits from the Weather Research and Forecasting Model [17]. Many items of free simulation code are also available for purely scientific purposes. Clustal [18] and Emboss [19] are suites for molecular genetic simulations. APBS [20] is a program that can compute the electrochemical properties and processes of biomolecules (see Figure 4). In the field of physics, Cernlib [21] is a collection of libraries and modules made available by the CERN physics lab.
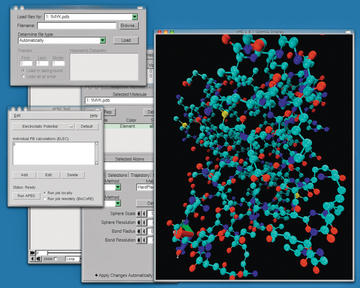 Figure 4: A protein molecule shown in VMD. VMD can interact directly with the APBS simulation software.
Figure 4: A protein molecule shown in VMD. VMD can interact directly with the APBS simulation software.
A handful of projects specialize in helping you convert your cluster into a rendering farm. POV-Ray [22] has supported distributed execution for many years. Also, the free 3D modeler Blender can export to the POV-Ray format or handle parallel rendering itself thanks to DrQueue [23], an open source tool designed for managing a rendering farm.
Parallel Programming
If you are working on a very specific problem, often the only solution is to write the software yourself or to parallelize an existing program. One important paradigm for creating distributed computer systems is the Message Passing Interface (MPI), a complete programming model that supports communications between parallel processors. MPI often provides the driver interface for the high-speed networks used by large-scale parallel computers. Free MPI implementations include Open MPI [24] or MPICH2 [25].
Another popular paradigm is OpenMP. The OpenMP programming model mainly relies on parallel programming of multiple core systems. Special pragma directives, which the programmer adds directly to the program code, tell the computer what it can automatically parallelize. Many compilers, including GCC, offer native support for OpenMP directives.
Open Computing Language (OpenCL) has recently gained traction as an important option for cross-platform parallel computing. You’ll get a close look at coding with OpenCL in the next article in this supplement. n
Info
[1] FAI:
[http://fai-project.org/]
[2] Partimage:
[http://www.partimage.org/Main_Page]
[3] SystemImager:
[http://wiki.systemimager.org/index.php/Main_Page]
[4] Parallel SSH:
[http://www.theether.org/pssh]
[5] Lm_sensors:
[http://www.lm-sensors.org]
[6] Smartmontools:
[http://sourceforge.net/apps/trac/smartmontools]
[7] Ganglia:
[http://ganglia.sourceforge.net]
[8] Software Raid How-to:
[http://tldp.org/HOWTO/Software-RAID-HOWTO.html]
[9] LVM2 Resource:
[http://sourceware.org/lvm2]
[10] CEPH:
[http://ceph.newdream.net]
[11] OpenPBS:
[http://www.mcs.anl.gov/research/projects/openpbs]
[12] Torque:
[http://www.clusterresources.com/products/torque-resource-manager.php]
[13] OpenCCS:
[https://www.openccs.eu/core]
[14] DistCC:
[http://code.google.com/p/distcc]
[15] R:
[http://www.r-project.org]
[16] Elmer:
[http://www.csc.fi/english/pages/elmer]
[17] WRF:
[http://www.mmm.ucar.edu/wrf/users]
[18] Clustal:
[http://www.clustal.org]
[19] Emboss:
[http://emboss.sourceforge.net]
[20] APBS:
[http://www.poissonboltzmann.org/apbs]
[21] Cernlib:
[http://wwwasd.web.cern.ch/wwwasd]
[22] POV-Ray:
[http://www.povray.org]
[23] DrQueue:
[http://www.drqueue.org/cwebsite]
[24] Open MPI:
[http://www.open-mpi.org]
[25] MPICH2:
[http://www.mcs.anl.gov/research/projects/mpich2]
The Author
Dominic Eschweiler is a member of the scientific staff at the Supercomputing Center of the Jülich Research Center. He mainly focuses on automated performance analysis of highly scalable parallel code.