Processor Affinity for OpenMP and MPI

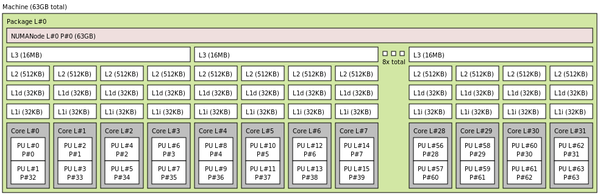
In a previous article, I discussed with simple examples how you might use two important affinity commands – taskset and numactl. However, I did not indicate how you might use these commands with various HPC applications. In this article, I present examples for (1) serial applications, (2) OpenMP applications, and (3) MPI applications. I’ll use the same architecture as before: a single-socket system with an AMD Ryzen Threadripper 3970X CPU that has simultaneous multithreading (SMT) turned on. Figure 1 shows the output from the lstopo command showing the layout of the processor. You can find more details on the test system in the previous article.

Figure 1: Output from lstopofor sample system.

Serial Applications

Serial applications use a single core. Although you might say that, given the large number of cores on modern systems, worrying about how a process uses a single core is not important, memory bandwidth could definitely suffer if the process is moved to a different NUMA node, causing the process to access memory across the CPU bus. Remember, in HPC you want your applications to run as fast as possible. Therefore, getting the best performance from serial applications is important.

One way to achieve this is to use taskset as part of the command to run the applications:

$ taskset --cpu_list 2 application.exe

This command sets the affinity of the application to core 2 and executes application.exe. You could have also used -c in place of --cpu_list to shorten the command.

Note that the use of taskset doesn’t set any sort of memory affinity, but this shouldn’t be a problem with a single process. If, for some reason, you need to move the process, you can use the taskset command with the process ID (PID) of the application.

If you want the best performance, you should use a “primary” core instead of an “SMT” core. However, if you are using all of the primary cores for something else (e.g., another application), you could always run on an SMT core, which might also be worthwhile if you have an application that isn’t really driven by memory bandwidth or floating-point operations. You could run the computationally intensive application on a primary core and the application that isn’t as computationally intensive on the SMT core of the pair. Just remember that memory bandwidth could suffer in this scenario.

A word of caution about picking cores for affinity: Some applications, such as storage clients or independent software vendor (ISV) applications, will pin processes to cores. If you try to run on an already pinned core, you could have issues, particularly if you try to pin your process to that core. Before you start binding to cores, be sure to look at the process table of the system for any processes that don’t appear to be system services, examine them with the taskset command, and look for information that indicates they are pinned already and to what core. Note the PID of the particular process and use the command:

$ taskset -cp <PID>

The -c option helps so you don’t have to read hexadecimal (even if you can).

Instead of taskset, you can use numactl to run serial applications, giving you additional control over where memory is allocated, as in this simple example:

$ numactl --physcpubind=2 --localalloc application.exe

The kernel scheduler will bind application.exe to core 2 and allocate memory by using the local NUMA node (node 0 for the sample system). You could reduce the length of the command as well:

$ numactl -C 2 -l application.exe

This command is very similar to taskset, but you cannot use numactl to move the process to another core once you’ve started it; however, you can start the process and then use taskset to move it to another core. If you move a process, keep it within the same NUMA node because you use the option --localalloc so memory bandwidth does not suffer.

The same general recommendations for running serial applications with numactl are the same as those for taskset; that is, keep memory access as close as possible to the core that is being used. Check any processes that don’t appear to be system processes before pinning applications, because running on a core that already has an application pinned to it could lead to issues, especially if you try to pin to that core.

An additional consideration, as mentioned previously, is whether to run the application on a primary or an SMT core. If you know your application doesn’t use floating-point computations heavily or use a great deal of memory bandwidth, then run it on a primary core or an SMT core. When in doubt, just pin the process to a primary core.

Pinning/Binding for OpenMP Threads

The use of processor affinity with OpenMP is interesting because the application may create and destroy threads during the application run. Informing the execution environment how and where to place the threads is important for the best performance. Some nonstandard ways of defining affinity are particular to specific compilers if you care to use those, but I won’t be covering them in this article. Fortunately, beginning in OpenMP 3.1, the standard published methods for affinity for OpenMP applications.

A good place to start is with the environment variable OMP_PROC_BIND that informs the execution environment how threads are bound to what is called “OpenMP places.” The second environment variable, OMP_PLACES, obviously describes the OpenMP places.

OMP_PROC_BIND has several possible values:

• false: If false, the OpenMP threads can be moved between OpenMP places (i.e., no affinity). If any code within the application attempts thread binding, it is ignored.
• true: If true, the OpenMP threads will not be moved between OpenMP places (no core migration). The initial thread of the application is placed in the first position in the OpenMP places list before any parallel region in the code is encountered.
• master: The master value collocates threads with the primary thread (most likely resulting in oversubscription of the core where the primary thread is run).
• close: The close value places the threads closest to the primary thread in the OpenMP places list, filling the first socket, in the case of a two-socket system, before moving to the second socket.
• spread: The spread value spreads out the threads as much as possible in an even manner. Depending upon the values in OMP_PLACES, it could be used to place processes in a two-socket system in a round-robin fashion.

The default value is true.

OMP_PROC_BIND can have multiple values in a command-separated list, but only with the values of master, close, and spread:

setenv OMP_PROC_BIND "spread, spread, close"

If the environment variable is set to true or false, there is only one value.

The second environment variable, OMP_PLACES, provides a list of values that are used for placing threads. From the OpenMP specification: “The value of OMP_PLACES can be one of two types of values: either an abstract name that describes a set of places or an explicit list of places described by non-negative numbers.” In this article, I won’t go in detail on the possible values because it can get quite complicated, so please consult the link to the specification to learn more. However, I will present a few simple examples.

The abstract values are,

• threads: Each place corresponds to a single hardware thread.
• cores: Each place corresponds to a single core that can have one or more hardware threads.
• sockets: Each place corresponds to a single socket that can have one or more cores.

To better understand how these options work, I’ll look at some simple examples.

Scenario 1

If the environment variable is set as OMP_PLACES=sockets and the system has two sockets, then the following happens:

• Thread 0 is placed on socket 0
• Thread 1 is placed on socket 1
• Thread 2 is placed on socket 0
• Thread 3 is placed on socket 1
• and so on …

That is, the threads are placed on sockets in a round-robin fashion. Note that nothing is stated about which cores on the socket are used, which allows the kernel scheduler to move the threads on the specific socket.

You could use this approach if you want to spread out the processes to get maximum memory bandwidth. However, it does not specify how the processes are bound in the socket, so the kernel scheduler could move them around (perhaps not the most ideal situation).

This approach is good if you need the greatest possible memory bandwidth, you don’t mind that processes get moved within a socket, the threads share very little data, there is not much synchronization, or the threads run longer than the time to synchronize to minimize the effect of synchronization on performance.

Scenario 2

The second example has the environment values:

setenv OMP_PROC_BIND cores
setenv OMP_PLACES close

On a system with two sockets, where each socket has n cores, the threads are placed in the following manner:

• Thread 0 is placed on core 0, socket 0
• Thread 1 is placed on core 1, socket 0
• Thread 2 is placed on core 2, socket 0
• and so on until all n cores on socket 0 are used

Then,

• Thread n+1 is placed on core n+1, socket 1 (socket 0 is full)
• Thread n+2 is placed on core n+2, socket 1 (socket 0 is full)
• and so on …

The environment variables force the “places” to be “close” to the primary thread, where places are cores. Therefore, successive cores are used for placing the threads, in order, starting with socket 0, filling it up, then moving to socket 1.

This approach would be good for OpenMP applications with a good amount of data sharing, synchronization, or both; not as much memory bandwidth is needed because the threads are packed into a single socket, reducing the memory bandwidth per thread. It forces the kernel scheduler not to move processes, saving the time it takes to move them. Also, because the threads are within the same socket, they don’t have to traverse the CPU connection, potentially improving communication performance.

If the application is very memory bandwidth intensive, then this approach has a downside, in that the first group of threads share the bandwidth. For example, if each socket has n cores and the application only uses n-2 cores, then all of the cores would share the memory bandwidth on socket 0 – not even using socket 1.

You would also get unbalanced memory performance if the application used n+n/2 threads, because socket 0 would have n threads and socket 1 would have n/2 threads. Again, if the application is memory bandwidth driven, then some of the threads would have much less bandwidth than other threads, creating unbalanced performance.

Scenario 3

The third example has the following environment values:

setenv OMP_PROC_BIND spread
setenv OMP_PLACES cores

For a two-socket system with n cores on each socket, the OpenMP threads are placed in the following manner:

• Thread 0 goes to core 0, socket 0
• Thread 1 goes to core n+1, socket 1
• Thread 2 goes to core 1, socket 0
• Thread 3 goes to core n+2, socket 1
• and so on …

The environment variables force the places to be spread apart as much as possible, where places are cores. Therefore, the cores are placed on socket 0, then socket 1, socket 0, socket 1, etc., in a round-robin fashion. On these sockets, the cores are used in order: core 0 on socket 0, followed by the first core on socket 1 (core n+1), followed by core 1 on socket 0, followed by the second core on socket 1, and so on.

This approach maximizes the memory bandwidth to each thread while making sure the thread stays bound to specific cores – all of which improves performance, unless the threads do a great deal of communication or synchronization that now has to cross the inter-CPU connection, which will reduce performance.

Scenario 4

The fourth example has the following environment values:

setenv OMP_PLACES "{0},{1},{2},{3}"

The OpenMP threads are placed in the following manner:

• Thread 0 goes to core 0, socket 0
• Thread 1 goes to core 1, socket 0
• Thread 2 goes to core 2, socket 0
• Thread 3 goes to core 3, socket 0

Notice that this layout is limited to four OpenMP threads, although you could easily extend because the pattern is pretty obvious.

You could also write the environment variable as one of the following:

setenv OMP_PLACES "{0,1,2,3}"
setenv OMP_PLACES "threads(4)"
setenv OMP_PLACES threads

The first two variable definitions indicate that the first four threads use the first four single hardware threads, but it is limited to four threads. I believe after four threads the remaining processes will be placed according to the defaults (be sure to consult the documentation for the compiler you are using and correct me if I’m incorrect). The third definition places the processes to single hardware threads with no restriction on the number of processes.

This approach gives you great control over thread placement, but you have to know how many threads the application uses to be specific, or you just use the keyword threads.

For more control, you can use just OMP_PLACES to place the threads on specific cores in whatever order you want to achieve the best performance for your OpenMP application.

A good site for OpenMP thread examples is Glenn Klockwood’s site.

Which placement strategy you use depends on your application. Be sure to understand two things: Is your application memory bandwidth bound? Is there a lot of communication, synchronization, or both between threads? If memory bandwidth is extremely important and there is little communication or synchronization, then a binding strategy similar to the third scenario typically works well.

If the application does a fair amount of communication or synchronization but is not that affected by memory bandwidth, then a placement strategy similar to the second scenario typically works best, because the effect of communication across the CPU interconnect is reduced.

If your application is a mix of being memory bandwidth limited but still does a fair amount of communication, then you will have to experiment with different thread placement strategies to find one that works best for you. I would recommend trying the second and third strategies as tests to understand how memory bandwidth and thread communication- and synchronization-focused strategies affect your application. Then, perhaps, you could use the fourth scenario to fine tune thread placement.

MPI Pinning/Binding Processes

MPI is a very common approach for writing multinode parallel applications, particularly in HPC. Binding MPI processes to CPUs can be just as important as for serial and OpenMP applications for the same reasons.

Several open source and commercial MPI libraries exist; I don’t have space to write about all of them, so I focus on two open source libraries – Open MPI and MPICH – but I also talk about Slurm because you can use it to bind cores for better performance.

Open MPI

Fortunately, Open MPI has support for CPU affinity and memory affinity. The first step in using Open MPI is to make sure it has been built with affinity support. According to the FAQ, “In general, processor affinity will automatically be built if it is supported – no additional command line flags to configure should be necessary.”

Affinity in Open MPI can be used in many ways for a wide variety of situations that can get very complex, depending on which way you chose to go. Of course, you can choose any of the methods for a number of reasons, but I like to keep things simple, so I will discuss the simplest way, in my opinion, to set affinity with Open MPI.

The simplest way to bind processes to cores is to use one of the following options in conjunction with mpirun: --bind-to core, --bind-to-core, or -bind-to-core (the last two deprecated in favor of the first). By adding one of these options to the mpirun command, the MPI processes will be bound to a core on the host nodes.

Personally, I like to bind to cores, but it could be problematic in some cases for performance reasons. The mpirun man page currently recommends this option only for one or two processes per node and recommends --bind-to socket if you have more than two processes per node. This approach allows the kernel scheduler to move processes from core to core on the particular socket as needed. I don’t know the details on how Open MPI binds processes to sockets, but I assume it uses round robin. If this is true, then the result is maximum memory bandwidth for the processes (in the case of a two-socket node). Other options, including caches, can be specified (see the mpirun man page) as --bind-to <target>.

When you are using any sort of affinity (binding) with Open MPI, it is a good practice to add the option --report-bindings to the mpirun command to see the binding information for your application.

You can use alternative ways to define process affinity, as well. One way involves “mappings” and another involves “rankings.” You can read about them on the mpirun man page, but I won’t discuss them here.

MPICH

Another popular MPI implementation is MPICH, which has a process affinity capability easiest to use with the Hydra process management framework and mpiexec. As with Open MPI, MPICH has several ways to define process affinity that can be found by reading the mpiexec man page. Listing 1 shows the output from the latest version of MPICH that I built on my test system. Notice the memory binding options (-membind).

Listing 1: mpiexec Help Output

$ mpiexec --bind-to -help

-bind-to: Process-core binding type to use

    Binding type options:
        Default:
            none             -- no binding (default)

        Architecture unaware options:
            rr               -- round-robin as OS assigned processor IDs
            user:0+2,1+4,3,2 -- user specified binding

        Architecture aware options (part within the {} braces are optional):
            machine          -- bind to machine
            numa{:}       -- bind to 'n' numa domains
            socket{:}     -- bind to 'n' sockets
            core{:}       -- bind to 'n' cores
            hwthread{:}   -- bind to 'n' hardware threads
            l1cache{:}    -- bind to 'n' L1 cache domains
            l1dcache{:}   -- bind to 'n' L1 data cache domain
            l1icache{:}   -- bind to 'n' L1 instruction cache domain
            l1ucache{:}   -- bind to 'n' L1 unified cache domain
            l2cache{:}    -- bind to 'n' L2 cache domains
            l2dcache{:}   -- bind to 'n' L2 data cache domain
            l2icache{:}   -- bind to 'n' L2 instruction cache domain
            l2ucache{:}   -- bind to 'n' L2 unified cache domain
            l3cache{:}    -- bind to 'n' L3 cache domain
            l3dcache{:}   -- bind to 'n' L3 data cache domain
            l3icache{:}   -- bind to 'n' L3 instruction cache domain
            l3ucache{:}   -- bind to 'n' L3 unified cache domain
            l4cache{:}    -- bind to 'n' L4 cache domain
            l4dcache{:}   -- bind to 'n' L4 data cache domain
            l4ucache{:}   -- bind to 'n' L4 unified cache domain
            l5cache{:}    -- bind to 'n' L5 cache domain
            l5dcache{:}   -- bind to 'n' L5 data cache domain
            l5ucache{:}   -- bind to 'n' L5 unified cache domain
            pci:         -- bind to non-io ancestor of PCI device
            gpu{|:}   -- bind to non-io ancestor of GPU device(s)
            ib{|:}    -- bind to non-io ancestor of IB device(s)
            en|eth{|:} -- bind to non-io ancestor of Ethernet device(s)
            hfi{|:}   -- bind to non-io ancestor of OPA device(s)


-map-by: Order of bind mapping to use

    Options (T: hwthread; C: core; S: socket; N: NUMA domain; B: motherboard):
        Default: 

        Architecture aware options:
            machine          -- map by machine
            numa{:}       -- map by 'n' numa domains
            socket{:}     -- map by 'n' sockets
            core{:}       -- map by 'n' cores
            hwthread{:}   -- map by 'n' hardware threads
            l1cache{:}    -- map by 'n' L1 cache domains
            l1dcache{:}   -- map by 'n' L1 data cache domain
            l1icache{:}   -- map by 'n' L1 instruction cache domain
            l1ucache{:}   -- map by 'n' L1 unified cache domain
            l2cache{:}    -- map by 'n' L2 cache domains
            l2dcache{:}   -- map by 'n' L2 data cache domain
            l2icache{:}   -- map by 'n' L2 instruction cache domain
            l2ucache{:}   -- map by 'n' L2 unified cache domain
            l3cache{:}    -- map by 'n' L3 cache domain
            l3dcache{:}   -- map by 'n' L3 data cache domain
            l3icache{:}   -- map by 'n' L3 instruction cache domain
            l3ucache{:}   -- map by 'n' L3 unified cache domain
            l4cache{:}    -- map by 'n' L4 cache domain
            l4dcache{:}   -- map by 'n' L4 data cache domain
            l4ucache{:}   -- map by 'n' L4 unified cache domain
            l5cache{:}    -- map by 'n' L5 cache domain
            l5dcache{:}   -- map by 'n' L5 data cache domain
            l5ucache{:}   -- map by 'n' L5 unified cache domain
            pci:         -- map by non-io ancestor of PCI device
                                (must match binding)
            gpu{|:}   -- map by non-io ancestor of GPU device(s)
                                (must match binding)
            ib{|:}    -- map by non-io ancestor of IB device(s)
                                (must match binding)
            en|eth{|:} -- map by non-io ancestor of Ethernet device(s)
                                (must match binding)
            hfi{|:}   -- map by non-io ancestor of OPA device(s)
                                (must match binding)


-membind: Memory binding policy

    Memory binding policy options:
        Default:
            none             -- no binding (default)

        Architecture aware options:
            firsttouch        -- closest to process that first touches memory
            nexttouch         -- closest to process that next touches memory
            bind:       -- bind to memory node list
            interleave: -- interleave among memory node list

To bind the processes to cores, use the command line:

$ mpiexec -bind-to core

In this case, core is the target binding. You could also easily bind to NUMA domains, sockets, a whole host of caches, PCI devices, GPUs, and Ethernet or InfiniBand interfaces. You can also bind with mappings (not covered in this article).

Finally, with the option -membind <policy>, memory allocation can be bound in some way. With the -membind bind option you can bind to a memory node list, as shown in the bottom of the mpirun help output in Listing 1. You can also use one of two policies for allocating memory.

As with Open MPI, I like to bind to cores, but you can also bind to other targets such as socket and numa nodes.

Slurm

For any application executed with Slurm, you can specify or modify bindings – but only if you use srun to execute your application. The processes can be bound to threads, cores, sockets, NUMA domains, and boards.

Defining bindings with srun can get complicated and, by now, you know that I will go for the simplest option in these situations. Although I haven’t used Slurm for running applications to bind to cores, in reading the man pages, I would start with the srun option:

$ srun --cpu-bind=cores,verbose ...

This option gives you lots of information about the CPU binding before executing the task. If you read the srun man page, you will see many more options. In the above example, srun uses the default bindings because I have only specified verbose.

Other options to use with --cpu-bind include sockets, cores, and threads. To bind to cores, use:

$ srun --cpu-bind=cores,verbose ...

Similarly, the command

$ srun --cpu-bind=sockets,verbose ...

binds to sockets.

Summary

People in HPC do almost everything possible to make their applications run faster, hence the moniker “High Performance.” With today’s complex systems with lots of cores, network interfaces, accelerators, memory channels, and local storage, finding combinations of these parameters with the performance you want is a difficult proposition. Making the problem even worse, the operating system likes to optimize its own performance so processes can be moved around, usually to the detriment of application performance.

Thankfully you have tools that allow you to place processes on specific CPU cores for the best performance. Two tools, taskset and numactl, were introduced in the previous article, and in this article, I presented how they can be used for running serial, OpenMP, and MPI applications. CPU affinity is important enough that the OpenMP standard and two of the prominent MPI libraries have incorporated affinity into their tools to make it easier for users. Moreover, Slurm has incorporated affinity into its tools for simple CPU affinity with any application that is launched with srun.

If you haven’t used CPU affinity before, as presented, it’s not that difficult to test, and it’s definitely worth testing your application with affinity.