The Python SymPy library for symbolic mathematics allows you to create complex mathematical expressions.
An Introduction to SymPy
SymPy is a computer algebra system written in the Python programming language. Among its many features are algorithms for computing derivatives, integrals, and limits; functions for manipulating and simplifying expressions; functions for symbolically solving equations and ordinary and partial differential equations; two- and three-dimensional (2D and 3D) plotting, and much more (e.g., see the SymPy features list and table 1 in a PeerJ Computer Science paper).
In this article, I use SymPy first for an algebraic function and then for the Fourier equation to explore heat conduction calculations. All the examples presented here use the Spyder 3.2.8 Python development environment (Anaconda 5.2.0) on Mint 19.0 Xfce. Because the full code is too long for a printed article, it’s freely available on GitHub. Python’s reserved words are not classified (e.g., as in Scilab), so I use “command” as a synonym of “reserved word.”
Algebraic Function
To carry out an algebraic calculation, you must define symbolic variables with thesymbolscommand, which returns a sequence of symbols with names taken from the namesargument (def symbols(names, **args):), which can be a comma- or whitespace-delimited string or a string delimited in other ways (Table 1; also see Introduction to SymPy). Symbols also can define a parametric curve -- for example, uand vare the symbols and x, y,zare the coordinates, as f(u,v).
Table 1: symbolsAssignments
| Expression | Description |
| Comma-delimited arguments | |
| Space-delimited arguments | |
| Colon-delimited range | |
| Range assignment | |
| Assigned to different names | |
| Greek letters | |
| Long names |
According to the SymPy documentation, to view well-rendered equations, use theinit_printing()command in your script, which will automatically enable the best printer available in your environment (i.e., LaTeX, if previously installed). The rendering is very good even if LaTeX is not installed (Figure 1).
 Figure 1: This Spyder screenshot shows how well equations are rendered, even when LaTeX is not installed.
Figure 1: This Spyder screenshot shows how well equations are rendered, even when LaTeX is not installed.
Table 2: SymPy Commands
| Operation | Calculation | View |
| Integral | integ=integrate(f(x),x) | integ + Enter |
| First derivative | deriv=diff(f(x),x) | deriv + Enter |
| Roots | roots=solve(deriv) | roots + Enter |
| 2D plot | — | plot(f(x),(x,xmin,xmax)) |
| 3D plot | — | plot3d(f,(x,xmin,xmax),(y,ymin,ymax)) |
Consider the algebraic function:
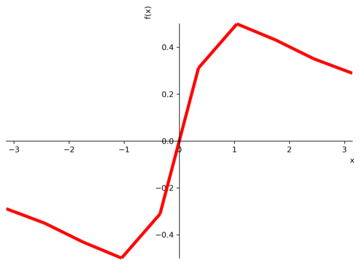
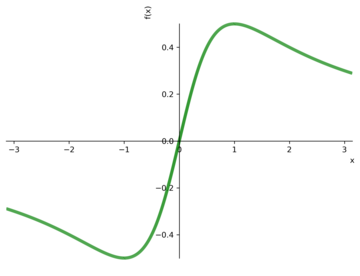
def f(x): return x/(x**2+1)
According to Table 2, the rootsare the x-coordinates of the minimum and maximum points, respectively. The two corresponding y-coordinates are then calculated by:
ymin=f(x).subs(x,const[0])ymax=f(x).subs(x,const[1])
Use ymin,ymax+Enter to view the result. Another way to calculate the two x-coordinates is with the use ofscipy.optimize.fmin:
from scipy.optimize import fmin xmin=fmin(f,0) xmax=fmin(lambda x: -f(x),0)
The indefinite integral is simply calculated as shown in Table 2. For the definite integral, you must specify the limits, for example,
integ=integrate(f(x),(x,xmin,xmax))
in which xminand xmaxare the interval limits. The definite integrals also can be calculated with scipy.integrate.quad. The plotcommand has the adaptiveoption set to Trueby default, so the resulting plot is segmented. If adaptiveis set toFalse, it’s possible to specify the number of points (nb_of_points) (Figures 2 and 3). Figure 4 shows the plot of a 3D function.
The most important thing to remember about plot3dis that the commandunset_show()must be called first to set line color, color map, and alpha values with _backend.ax.collections[0]. I have used the parulacolormap built from the parula.csv data. The complete scripts for these first two examples are function2d.py and function3d.py, respectively.
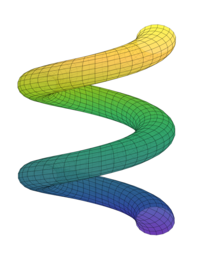
The mpmath.splot and plot3d_parametric_surface functions plot parametric surfaces. For example, a corkscrew surface (Figure 5) is defined and plotted by the code:
u,v=symbols("u,v")
x=cos(u)*(cos(v)+3)
y=sin(u)*(cos(v)+3)
z=sin(v)+u
plot3d_parametric_surface(x,y,z,(u,umin,umax),(v,vmin,vmax),...)The complete script for this example is corkscrew.py.
Flat Wall in Steady State
The Fourier equation is an example of a second-order (parabolic) partial differential equation (PDE). This equation is the fundamental tool for the study of thermal fields inside bodies. In practice, the Fourier equation integration is possible only in few cases, with a drastic simplification of the hypotheses. Two of these cases, important for technical applications, are examined in this section.
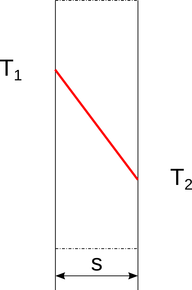
Consider a flat, homogeneous, infinite wall of constant thickness s (Figure 6) with faces of uniform temperatures in steady state (i.e., time independent). In this first case, the Fourier equation is:
where x=0 is the left side and x=s is the right side of the section. The plotcommand shows the linear relationship between T and x within the wall section (Figure 6, red line).
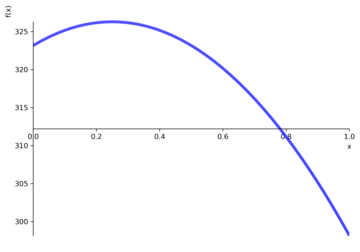
With internal heat generation, the Fourier equation becomes
in which H is the volumetric heat generation and lambda is the thermal conductivity of the wall. In this second case, the plot command shows the temperature in the wall as a parabolic trend (Figure 7). In both cases, the temperature trend is calculated by:
solut=dsolve(difeq,T(x)) const=solve([solut.rhs.subs(x,0)-T1,solut.rhs.subs(x,s)-T2]) funct=solut.subs(const)
The differential equation is solved by dsolve in the first line, the constants are calculated using its right-hand side (rhs) in the second line, and the final function is calculated in the third line. The funct function is plotted in the range from x=0 to x=s through the wall section. The complete script is fourier.py. To specify the boundary conditions, it’s also possible to usedsolvewith the ics={…} option, in which ics means initial conditions. At the present time, this option works only on particular cases, so it’s not for a general use.