« Previous 1 2 3
Web applications with Julia
On the Rise
A Final Example
One more example, expanding a bit on the previous one, will serve to demonstrate a few more controls and show how to use styles to lay out the page. Additionally, this example actually does something almost useful.
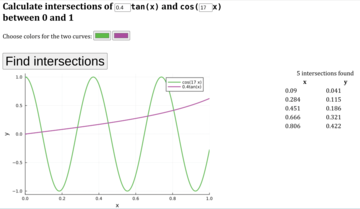
The mathematical problem of finding the intersections of trigonometric functions typically has only numerical solutions. Figure 6 is a browser screenshot showing an application that lets the user pick two parameters: one for the amplitude of the tangent function and the other for the frequency of a cosine function. The user can also select two colors with two color pickers. On clicking the Find intersections button, two new elements appear on the page: a graph of the two functions in the selected colors and a table listing all of their intersections within the range (0, 1).
Listing 5 contains the complete HTML code for the client page, aside from the header and other HTML administrivia, and Listing 6 has the complete server program.
Listing 5
Client for
01 <form data-hx-ext="ws" data-ws-send data-ws-connect="ws://127.0.0.1:8660"> 02 <h2>Calculate intersections of <code><input style='width:3em;' type="number" name="t" min="0.1" max="1" value='1' step='0.1'>tan(x)</code> and <code>cos(<input style='width:2.5em;' type="number" name="c" min="1" max="40" value='4'>x)</code><br> between 0 and 1</h2> 03 Choose colors for the two curves: 04 <input type='color' name='c1' value='#990000'> 05 <input type='color' name='c2' value='#000099'><br> 06 <input type='submit' style='font-size:2em; margin-top:1em;' value='Find intersections'><br> 07 <img alt='' src='' id='plot'> 08 <table id='ztable'></table> 09 </form>
Listing 6
Server for
01 using HTTP, JSON, Base64, Roots
02 const PORT = 8660
03
04 function startserver()
05 io = IOBuffer();
06 x = 0.0:0.001:1.0
07 WebSockets.listen("127.0.0.1", PORT) do ws
08 for msg in ws
09 lc1 = JSON.parse(msg)["c1"]
10 lc2 = JSON.parse(msg)["c2"]
11 c = Meta.parse(JSON.parse(msg)["c"])
12 t = Meta.parse(JSON.parse(msg)["t"])
13 f1(x) = cos(c * x)
14 f2(x) = t * tan(x)
15 f(x) = f1(x) - f2(x)
16 z = round.(find_zeros(f, (0, 1)), digits=3)
17 y = round.(f1.(z), digits=3)
18 ztable = []
19 for zero in zip(z, y)
20 append!(ztable, "<tr><td>$(zero[1])</td><td>$(zero[2])</td></tr>")
21 end
22 ztable = join(ztable)
23 p = plot([f1 f2]; xrange=(0, 1), lc=[lc1 lc2], lw=2, xlabel="x", ylabel="y", label=["cos($c x)" "$(t)tan(x)"])
24 show(io, MIME"image/png"(), p)
25 data = base64encode(take!(io))
26 WebSockets.send(ws, """<img data-hx-swap-oob='true' id='plot' src='data:image/png;base64,$data' alt='sin(1/x)'>""")
27 WebSockets.send(ws, """<table data-hx-swap-oob='true' id='ztable' style='width:13em; float:right;'> <caption> $(length(z)) intersections found </caption> <tr><th>x</th><th>y</th></tr> $ztable </table>""")
28 end
29 end
30 end
By this point, the function of most of what's in these programs should be clear. The server code contains nothing fundamentally new: just some additional variables and the use of the Roots
package [23] to calculate the function intersections. Note the inclusion of style attributes in the returned HTML fragments and the incorporation of variables in plot labels and the table caption. The first two lines in the outer for loop extract the two variables set by the color selectors, leaving them as strings for direct insertion in the plot() call.
Listing 5 illustrates the use of forms with HTMX. Rather than placing the HTMX communication attributes in an input element as you saw in Listing 2, you can place them in an opening form tag. When the user hits the form submission button, all the variables defined by input controls within the form are sent over the WebSocket in a single message.
Go Forth and Code
The virtues that have made Julia so successful in the realm of scientific computing and engineering – ease of development combined with uncompromised performance – also make it a good choice for the back end of web applications. In this article, you've learned about two approaches to making interactive websites for education, information, and entertainment. You might decide to adopt one or the other (or neither!) or, like me, apply the two approaches to different projects. I've found working with Julia in concert with web technologies to be one of my most enjoyable and rewarding adventures in programming. I hope you will have as much fun as I did with my projects in building things that I can't imagine. Please share news of your creations by dropping me a line through email or in comments on my website.
Infos
- Julia language: https://julialang.org/
- "Fast as Fortran, Easy as Python" by Lee Phillips, ADMIN , issue 50, 2019, https://www.admin-magazine.com/Archive/2019/50/Julia-Fast-as-Fortran-easy-as-Python
- "New ways to compile Julia" by Jeff Bezanson, JuliaCon 2024 : https://info.juliahub.com/blog/new-ways-to-compile-julia-blog
- Phillips, Lee. Scientific computing's future: Can any coding language top a 1950s behemoth? Ars Technica , May 2014: http://arstechnica.com/science/2014/05/scientific-computings-future-can-any-coding-language-top-a-1950s-behemoth/
- Julia joins petaflop club, HPCWire , 2017, https://www.hpcwire.com/off-the-wire/julia-joins-petaflop-club/
- "Rankings of Julia Books on Amazon," by Lee Phillips, 2024: https://lee-phillips.org/amazonJuliaBookRanks
- Phillips, Lee. Practical Julia . No Starch Press, 2023: https://nostarch.com/practical-julia
- PlutoSliderServer.jl: https://github.com/JuliaPluto/PlutoSliderServer.jl
- Pluto.jl: https://github.com/fonsp/Pluto.jl
- htmx – High power tools for HTML: https://htmx.org/
- Jupyter: https://jupyter.org/
- "An Introduction to Pluto" by Lee Phillips, LWN.net , November 2020: https://lwn.net/Articles/835930/
- PlutoUI.jl: https://github.com/fonsp/PlutoUI.jl
- Pkg: https://docs.julialang.org/en/v1/stdlib/Pkg
- PlutoUI widgets: https://featured.plutojl.org/basic/plutoui.jl
- HypertextLiteral overview: https://juliapluto.github.io/HypertextLiteral.jl/stable
- systemd-nspawn: https://wiki.archlinux.org/index.php/Systemd-nspawn
- Javis: https://github.com/Wikunia/Javis.jl
- HTTP.jl: https://github.com/JuliaWeb/HTTP.jl
- htmx WebSocket extension: https://htmx.org/extensions/ws
- Data URLs: https://developer.mozilla.org/en-US/docs/Web/URI/Schemes/data
- Base64: https://developer.mozilla.org/en-US/docs/Glossary/Base64
- Roots.jl: https://github.com/JuliaMath/Roots.jl
- Phillips, Lee. Einstein's Tutor . PublicAffairs, 2024: https://www.amazon.com/gp/product/1541702956?tag=hacboogrosit-20
« Previous 1 2 3
Buy this article as PDF
(incl. VAT)
Buy ADMIN Magazine
Subscribe to our ADMIN Newsletters
Subscribe to our Linux Newsletters
Find Linux and Open Source Jobs
Most Popular
Support Our Work
ADMIN content is made possible with support from readers like you. Please consider contributing when you've found an article to be beneficial.